Voici les notes de 30 élèves à un devoir :
| 12 | 08 | 03 | 13 | 09 |
| 08 | 12 | 13 | 14 | 19 |
| 18 | 09 | 15 | 15 | 18 |
| 14 | 11 | 14 | 16 | 16 |
| 14 | 12 | 12 | 09 | 15 |
| 15 | 14 | 10 | 16 | 08 |
- Déterminer la moyenne de la classe.
- Déterminer l'écart type de ce devoir et en déduire si la dispersion est grande.
Résolution :
On crée le tableau suivant :
| Notes
xi |
Effectif :
ni |
|
|
| 03 | 1 | 3 | 1×3×3=9 |
| 08 | 3 | 24 | 3×8×8=192 |
| 09 | 3 | 27 | 3×9×9=243 |
| 10 | 1 | 10 | 100 |
| 11 | 1 | 11 | 121 |
| 12 | 4 | 48 | 576 |
| 13 | 2 | 26 | 338 |
| 14 | 5 | 70 | 980 |
| 15 | 4 | 60 | 900 |
| 16 | 3 | 48 | 768 |
| 18 | 2 | 36 | 648 |
| 19 | 1 | 19 | 361 |
| N = 30 | somme =382 | somme=5236 |
La moyenne est de
.
La
variance est
.
L'écart
type vaut donc :
.
L'écart type représente environ 25 % de la note moyen, ce qui est grand. On peut donc considérer que cette population est assez dispersée.
Un commerçant décide à la fin de la journée de calculer le montant moyen des chèques encaissés.
|
Montant des chèques en F |
Effectif ni |
| [ 0 ; 20 [ | 25 |
| [ 20 ; 40 [ | 40 |
| [ 40 ; 60 [ | 36 |
| [ 60 ; 100 [ | 4 |
Déterminer l'écart-type selon deux méthodes.
Résolution :
Méthode
1 en utilisant la formule de la variance :
.
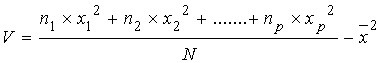Créons un tableau :
|
Montant des chèques en F |
Centre
de
classe : xi |
Effectif : ni |
|
|
| [ 0 ; 20 [ | 10 | 25 | 250 | 2500 |
| [ 20 ; 40 [ | 30 | 40 | 1200 | 36000 |
| [ 40 ; 60 [ | 50 | 36 | 1800 | 90000 |
| [ 60 ; 100 [ | 80 | 4 | 320 | 25600 |
| N = 105 | total = 3570 | total = 154100 |
La
montant moyen est
euros.
La
variance vaut donc
,
d'où s
= 18.
L'écart-type vaut donc 18 euros. On a donc une grande dispersion des valeurs.
Méthode
2 en utilisant la méthode de la variance
|
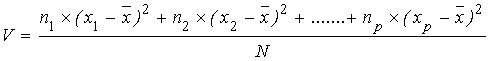
Montant des chèques en F |
Centre
de
classe : xi |
Effectif : ni |
|
|
| [ 0 ; 20 [ | 10 | 25 | 250 |
|
| [ 20 ; 40 [ | 30 | 40 | 1200 | 640 |
| [ 40 ; 60 [ | 50 | 36 | 1800 | 9216 |
| [ 60 ; 100 [ | 80 | 4 | 320 | 8464 |
| N = 105 | total = 3570 | total = 32720 |
La
montant moyen est
euros.
La variance vaut donc V = 32720 / 105 = 312, d'où s = 18.
: Les deux méthodes amènent aux mêmes résultats, on
choisira donc sa méthode pour calculer l'écart - type. Lors des examens, on
impose souvent la 1ère méthode.